By Thomas Beet //
What if we could ‘predict’ how long brains may perceive a Lissajous Curve? How would you feel if I told you that we are sort of there?
The goal of this project was to read a current quantum-like model of bistable perception, understand it and build an improved model before applying it to a mathematical curve known as a Lissajous curve: a curve of overlapping sine curves that the brain perceives to be rotating in three dimensions in this case, clockwise or anticlockwise. This model can be used to estimate how long a person may be able to perceive a certain direction of the curve before the brain ‘switches’ direction. All of this involves quantum probability and the quantum Zeno Effect.
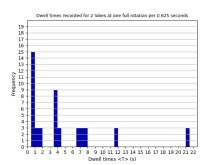Working with my supervisors, we read up on the previous literature and scrutinised the material. We discussed details such as variable names and meanings, the experiment performed to gather the data, and how we would produce the data. Further scrutiny was involved with this paper as the quantitative measurements and mathematical model to explain it were scarce and all papers relied on the same decades-old data.
From there on, the supervisors oversaw refining the model while I was in charge of experimental design and implementation (e.g. coding the curves and the experiment into Python). This felt like a genuine collaboration, and as a result it has helped me improve my problem-solving skills as well as my programming skills, giving me lots of independence; furthermore, my supervisors still gave me assistance when I needed it.
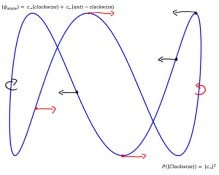The main challenge I experienced was producing the moving Lissajous curves at a high enough quality to use in the preliminary experiment. The only Lissajous curves available had a constant rotation speed, and consequently to create the videos I had to use ffmpeg – something I had never used before. Producing the videos took longer than expected as a result. However, with regular communication and help from my supervisors I was able to overcome these obstacles.
From this experience I have learnt how to properly manage my time to successfully complete my tasks at an optimal pace. Additionally, I have learnt how to better overcome obstacles that arise when trying to complete my project. For example, when I struggled to understand a concept or came across programming issues, I would break my tasks down into three or four smaller segments and switch between them, always keeping my brain active whilst reducing inactive periods.
As I am keen to work in academia after I graduate, I knew that applying for this research bursary would provide invaluable experience for me to help me achieve my goals after university. Especially since this research includes areas of Physics which I am very interested in pursuing.
*To view Thomas’s research poster and presentation recording, please click on the thumbnails below:
